How large models can abstract rules: a research by LIMS

Large language models possess remarkable capabilities in language comprehension, code generation, and various other tasks. However, a crucial question arises: How well can they abstract problem-solving rules and algorithms? More importantly, how can we effectively test this ability?

Let’s consider a simple example: the classic blocks world planning problem. This problem involves swapping colored blocks stacked on the tabletop. The task is to list the moves required to change a current state to a target state. We add a constraint similar to manipulating real blocks: at each step, you can only remove the top block and set it aside, or return a previously set-aside block to the top. When presented with this problem in natural language, GPT-4 achieves a modest success rate of about 40%.

Now, imagine we transform the concept of blocks, colors, and actions into something entirely different — say, elements from a fantasy world. The blocks become magical objects, colors represent various magical properties, and actions are spells. The fundamental task remains unchanged; we’ve merely relabeled the objects, properties, and actions. Surprisingly, GPT-4’s performance plummets dramatically to around 1% in this scenario.

If we take it a step further and replace the names with arbitrary character sequences of the same length, the performance drops to zero. Other models exhibit similar results.

This example highlights a reasoning weakness of LLMs where they fail, and humans significantly outperform AI. People can abstract the solution algorithm and apply it even to meaningless objects and actions. The ability to abstract is particularly crucial in mathematics. For instance, when working with a function of a variable, we aim to compute it for any value, not just those used during model training.

The blocks world example raises concerns about the capabilities of modern large language models in solving problems, which require reasoning and abstract thinking. Intrigued by this, researchers at LIMS sought to test how well the architecture of large language models can abstract rules. This inquiry focuses on the transformer architecture — the foundation of modern LLMs, which we’ve discussed in one of our blog posts. The LIMS scientists tackled this challenge using Nebius AI.

Elementary cellular automata emerged as an ideal testing tool for this purpose. These strictly defined mathematical objects are primitive enough that applying learning algorithms to them allows us to understand two things. First, can the model abstract the task when dealing with such a simple object? And second, if it can, how does it do it — in other words, how does the neural network learn to “distill” the rules?

A cellular automaton operates on a simple principle:

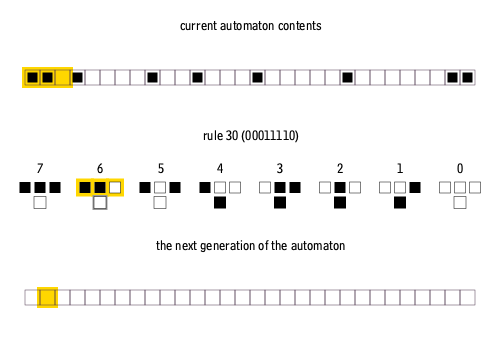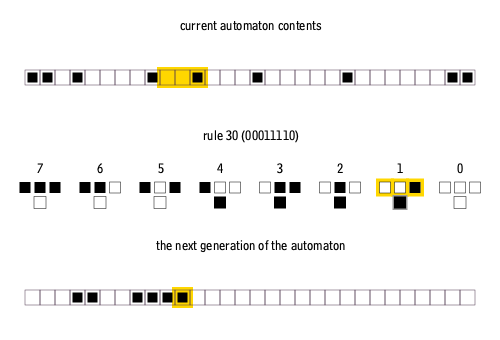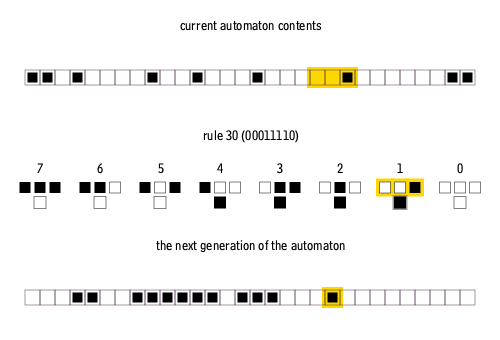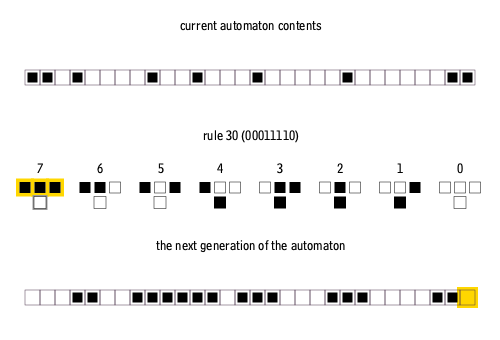
Why is this process relevant to the problem we formulated above? The middle part of the animation describes the rule by which the cellular automaton operates (which can be abstracted). We see the first row and the second row derived from it using the given rule. This process continues: the third row is generated from the second using the same rule, and so on, creating a sequence of binary strings that describe the automaton’s temporal evolution.

A well-known example of such a sequence is the Sierpinski triangle:

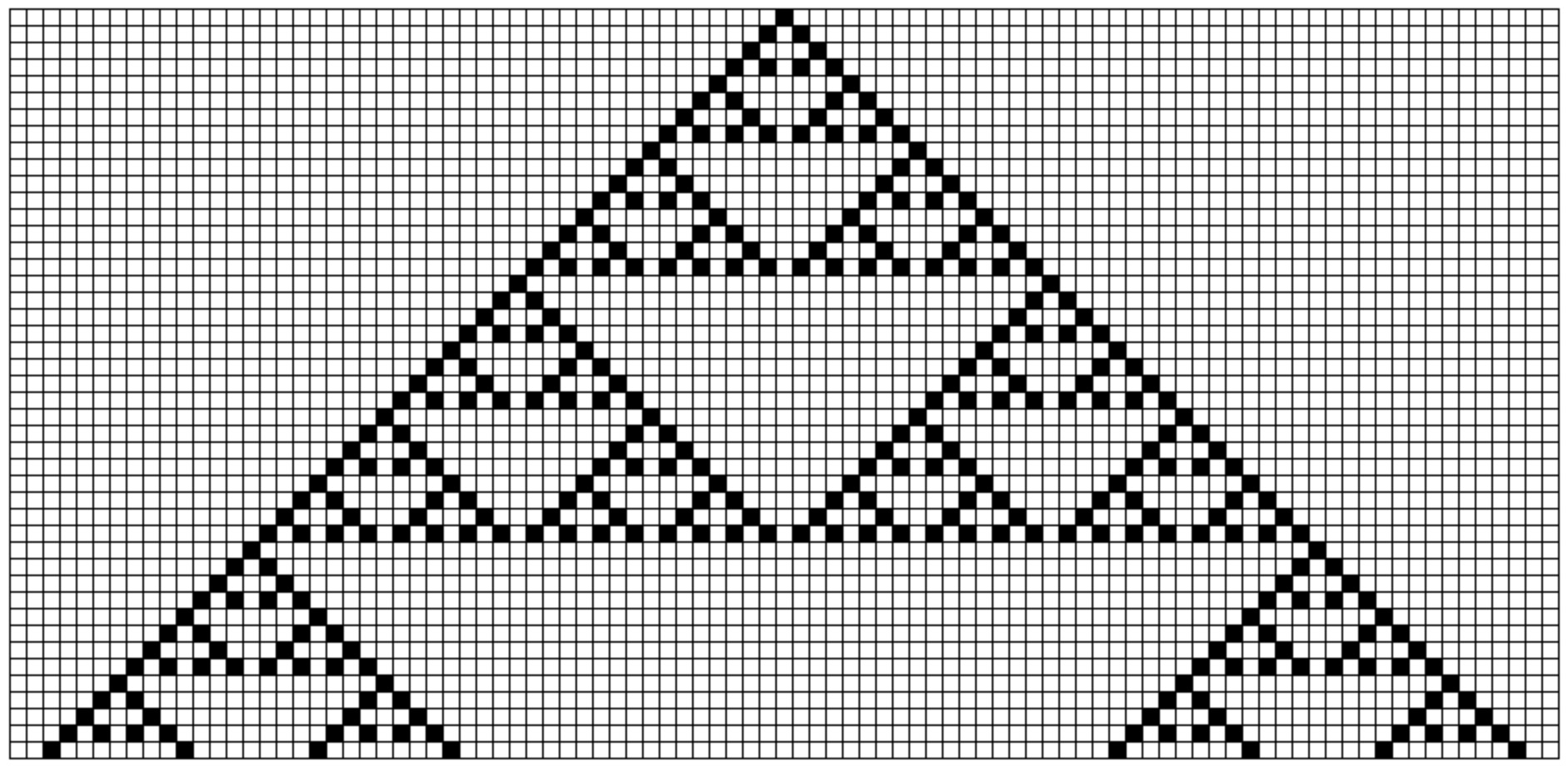
In the triangle’s first row, only one symbol is shaded. To form this image from a series of rows, a simple rule is applied:

Other examples exist, including those where the image evolution becomes seemingly unpredictable — each subsequent row appears to be generated randomly:

However, even in these cases, the rule remains strictly deterministic, illustrating the mathematical concept of “deterministic chaos.”

Now that we understand how cellular automata work, let’s explore the model chosen by our LIMS colleagues for testing and the principles behind its training.

They selected BERT, the first truly significant encoder transformer model, as the most suitable candidate. While less advanced than current models, BERT is ideal for testing whether transformers can abstract tasks.

Let’s examine a sequence generated by a rule with a radius of 1 (r1), where values are added within a distance of 1 from the central cell, resulting in 3 input variables:

Here, the rule 1100111 and row t = 0 are randomly generated, and each subsequent row up to row 5 is derived from the previous one by applying chosen rule. In LIMS’s first task, the BERT model is trained to predict the rule from these six consequent states. With 6 rows total, each 84 digits long, this variant is dubbed r1s84T6. Such dataset allows for 256 rules in total, presenting a relatively simple computational challenge.

LIMS researchers then increased the complexity. In the r2s84T6 task, they expanded the radius to 2, resulting in 5 variables:

This expansion allows for approximately 4 billion possible rules.

Pushing further, when the radius is increased to 3 with 7 variables, the number of possible rules skyrockets to about 10³⁸. The space of potential rules grows combinatorically. Consider the third variant, r3s24T20:

In this setup, the model trains on about a million different rules and is then tested on rules absent from the training set. During analysis, the model encounters each rule once in the training set but never sees them in the test set.

Here are some of the samples used for training:

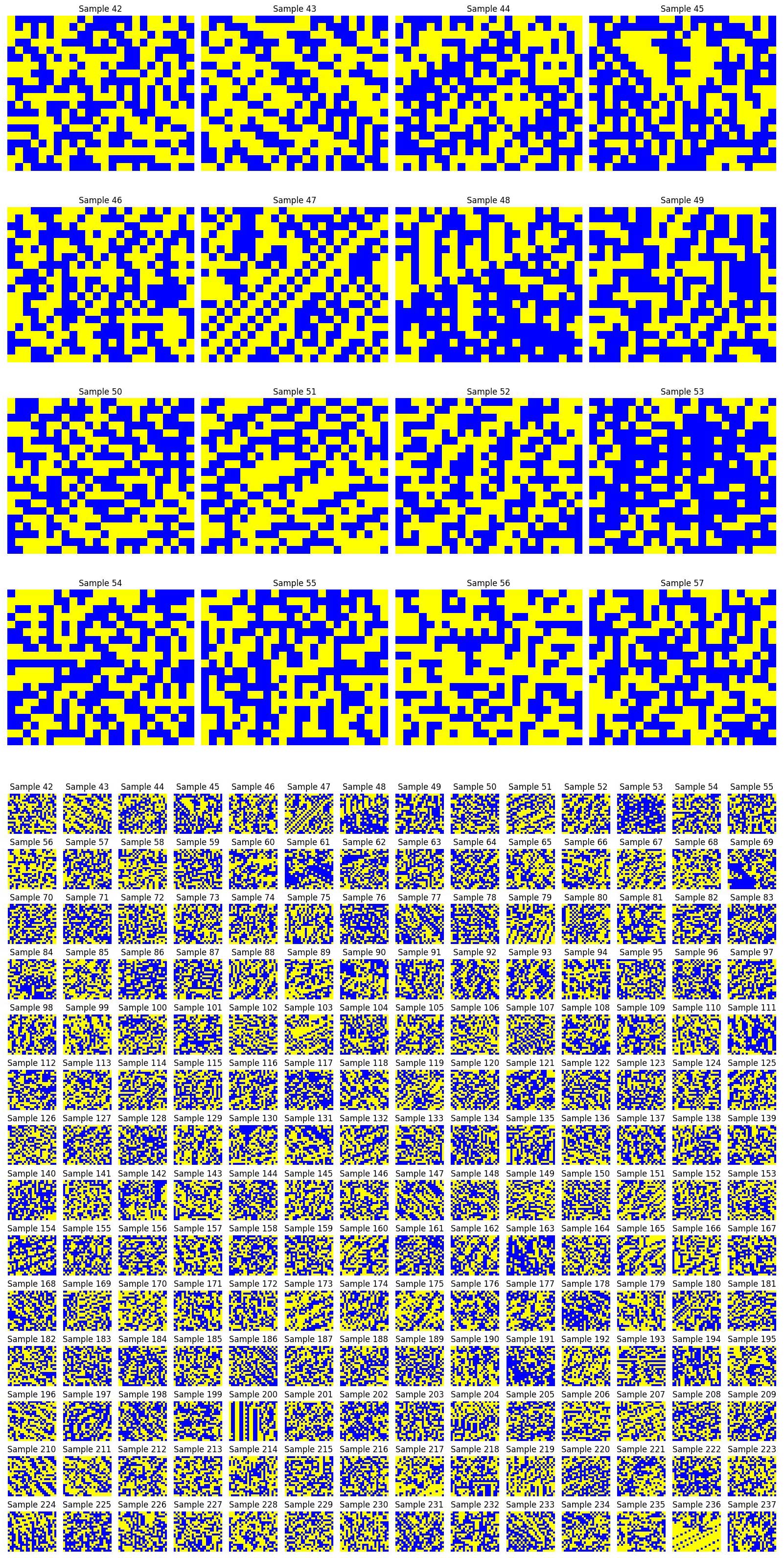
Can you, by looking at these samples, try to guess which rule has been used to generate them? This shows the complexity of the task.

The results obtained by LIMS are shown on the graph below:

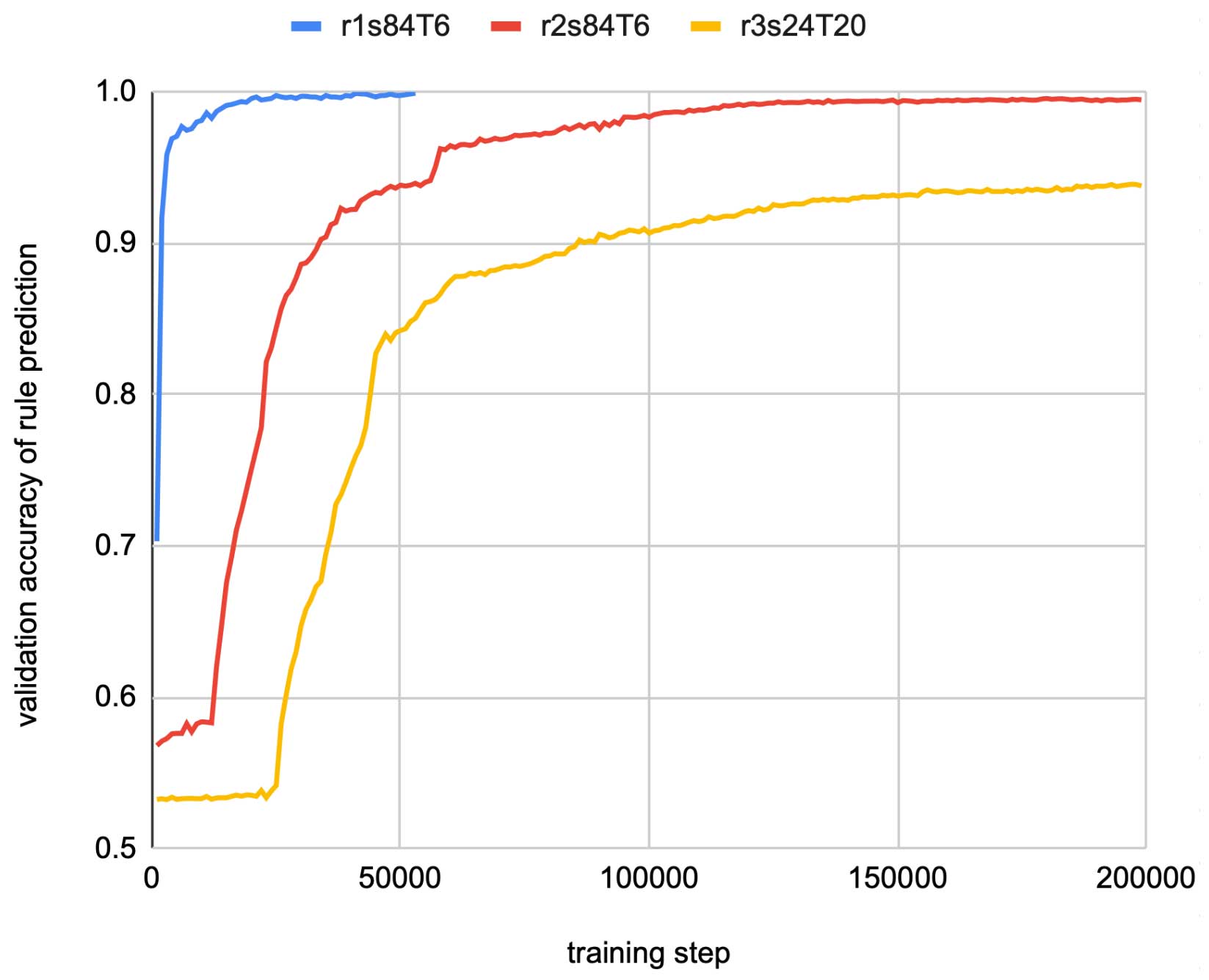
Getting a validation accuracy of more than 0.93, we can see that BERT can indeed successfully predict the rule, synthesizing from input data a program that generates this data. This implies that more advanced modern transformer neural networks are also capable of such abstraction.

While the blocks world example mentioned at the beginning remains valid, we now understand that LLMs’ inability to abstract tasks isn’t due to their architecture. Rather, it’s a consequence of their training specifics. We’re pleased that this scientifically significant result was achieved using the Nebius AI infrastructure, contributing to our understanding of AI capabilities and limitations.